Tutorials
Binary Search Trees
You should start by reading about binary search before reading this page. It assumes you understand that page.
Briefly, we applied binary search by recursively partitioning a sorted array into two pieces, doing one comparison, and then eliminating one (or both, if we found what we were looking for) partition.
Now lets consider a slightly different way of drawing the sorted array:
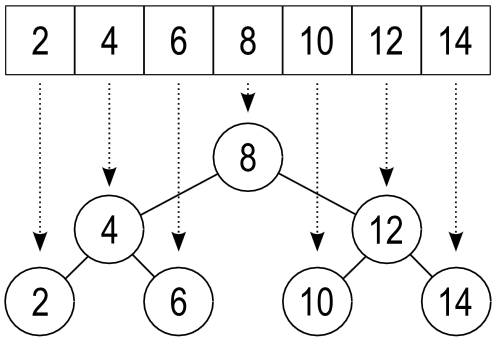
- This is actually much more than just redrawing the sorted array in a different way.
- You'll notice that as you work your way from left to right, the elements in the lower figure are still in sorted order.
- The bottom part of the figure represents a binary search tree.
- A binary search tree must adhere to the following rules:
- There is one element at the top, called the root
- Each element can have at most two elements directly below it, called children
- The left child must be less than its parent
- The right child must be greater than its parent1)
- Performing a binary search on a binary search tree is a simple matter of recursively working our way down the tree.
- If the element we are looking for is less than the current element, we go to the left child
- If the element we are looking for is greater than the current element, we go to the right child
- Otherwise, we have found our element and we are ready to stop
- If we make it to the bottom of the tree without encountering the value we are looking for, we can be certain that it is not present in our data structure.
Tree Terminology
- A tree is said to be a binary tree if each element can have zero, one, or two children.
- Each element in the tree is called a nest2)
- The top-most nest is called the root.
- The root and all of the nests connected to it are called a tree.
- Any nest and all of the nests connected below it are called a subtree.
- A nest directly above another nest is called its parent.
- A nest directly below and to the left of another nest is called its left child.
- A nest directly below and to the right of another nest is called its right child.
- A tree is said to be a binary search tree if every left child is smaller than its parent and every right child is larger than its parent.
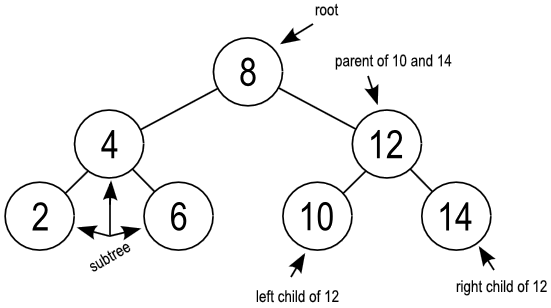
- A nest with no children is called a leaf.
- The height of the tree is typically defined the number of levels below the root.3) E.g., an empty tree has a height of -1, a tree with just one element has a height of 0, and tree with a root and one child has a height of 1.
- A tree is said to be perfect if for every level except the bottom level, every nest has two children.
- A tree is said to be complete if every level, except possibly the last, is completely filled, and all nests are as far left as possible.
- There are various definitions for a balanced tree.4)
- Some say that in order for a tree to be balanced the distance from the root to any leaf in the tree must differ by no more than one.
- A looser definition is also acceptable: A balanced tree is one in which the distance from the root to any leaf differs by no more than a fixed constant multiple. Often this multiple is two, implying that the longest distance from root to leaf may be no more than two times the shortest distance from root to leaf.
1)Are you wondering what happens if you have two elements with the same value? If not, are you wondering why you are not wondering that? If not, repeat previous statement. Same valued entries are not allowed in a binary search tree. I.e., the values of all elements in a binary search tree must be unique.
2)Actually, most people call them nodes, but when I was explaining binary search trees to my 10-year-old, he thought they should be called nests. It sounded good to me, so that's what I'm calling them today.
3)Although our current textbook defines it as one more than this.
4)Sometimes balanced trees are called height-balanced trees to more clearly specify what about the tree is balanced.
2)Actually, most people call them nodes, but when I was explaining binary search trees to my 10-year-old, he thought they should be called nests. It sounded good to me, so that's what I'm calling them today.
3)Although our current textbook defines it as one more than this.
4)Sometimes balanced trees are called height-balanced trees to more clearly specify what about the tree is balanced.
Last modified: Monday, 29-Jul-2024 06:54:30 EDT