Introduction
Java is an object oriented (OO) programming language. The key idea behind object oriented programming is to identify objects that need to be represented in your program and then group all of the data associated with the object in a blob of bytes. In addition, we can define behavior that will operate on the the blob of data. This allows us to simplify our programs because all of the code associated with defining and managing the objects can be placed in a separate source file. Only the implementer(s) of the class need to worry about the details of how the objects are stored (what attributes are required) and manipulated (the implementation of methods defining desired behavior).
Object Free Messiness
Suppose we want a program that asks the user to enter two complex numbers and displays the result of multiplying the two complex numbers together. It might look something like this:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// Get first number
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
String line = in.nextLine();
Scanner parser = new Scanner(line.substring(0, line.length()-1));
double realOne = parser.nextDouble();
parser.next();
double imagOne = parser.nextDouble();
// Get second number
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
line = in.nextLine();
parser = new Scanner(line.substring(0, line.length()-1));
double realTwo = parser.nextDouble();
parser.next();
double imagTwo = parser.nextDouble();
// Calculate result of multiplying two numbers
double realAnswer = realOne * realTwo - imagOne * imagTwo;
double imagAnswer = realOne * imagTwo + imagOne * realTwo;
System.out.println("(" + realOne + " + " + imagOne + "i) * ("
+ realTwo + " + " + imagTwo + "i) = ("
+ realAnswer + " + " + imagAnswer + "i)");
}
This produces a result that looks like this:
Enter a complex number in the form: 3.0 + 4.3i 1.0 + 3.0i Enter a complex number in the form: 3.0 + 4.3i 2.0 + 2.0i (1.0 + 3.0i) * (2.0 + 2.0i) = (-4.0 + 8.0i)
Object Oriented Clarity
This code above looks pretty complicated because our main method is
required to manage all of the intricate details of complex numbers.
The rest of this page will focus on developing a Complex
class that will define all of the code specific to managing complex
numbers. When completed, it will allow us to simplify our program so
that it looks like:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// Get first number
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c1 = new Complex(in.nextLine());
// Get second number
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c2 = new Complex(in.nextLine());
// Calculate result of multiplying two numbers
Complex answer = c1.times(c2);
System.out.println(c1 + " * " + c2 + " = " + answer);
}
In fact, the code is so much cleaner that we don't really need to include the comments. The intent of the code is so much clearer:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c1 = new Complex(in.nextLine());
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c2 = new Complex(in.nextLine());
System.out.println(c1 + " * " + c2 + " = " + c1.times(c2));
}
Defining Custom Classes
A user defined class should be in a separate file that has the
same name as the name of the class (the following would be stored
in a file called Complex.java). A class is defined
as follows:
public class Complex {
// Details of the class implementation go here
}
Object Attributes
We can declare attributes for each object from the class as follows:
public class Complex {
private double real;
private double imag;
// ...
}
Whenever we create an object from the Complex class,
the object will have two object variables: real and
imag (both doubles) that can be
used to store the value of a complex number. If we were to
create a Complex object like this:
public static void main(String[] args) {
Complex c1 = new Complex();
}
here's what it would look like in memory:
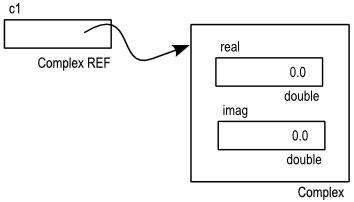
Constructors
Right now, we don't have a way to set the values of the object's attributes. One way to do this would be to implement a constructor that accepts real and imaginary values for the object that is about to be created. The implementation would take the values passed in and assign them to the object's attributes:
public class Complex {
private double real;
private double imag;
public Complex(double r, double i) {
real = r;
imag = i;
}
}
public static void main(String[] args) {
Complex c1 = new Complex(2.0, 1.0);
System.out.println(c1);
}
When the object is instantiated (created), space is reserved in memory to hold the object and then the constructor initializes the attributes of the object. Now the memory footprint for the instantiated object looks like this:
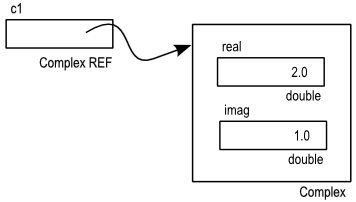
The output of the program is:
packageName.Complex@6ddf073d
where packageName is the name of the package containing
the Complex class.
The toString() Method
We can customize the way the object displays itself by implementing
the toString() method. The toString() method
returns a string representation of the object:
public class Complex {
private double real;
private double imag;
public Complex(double r, double i) {
real = r;
imag = i;
}
public String toString() {
return "(" + real + " + " + imag + "i)";
}
}
Now when we run the program, we see the following displayed:
(2.0 + 1.0i)
Adding Complex Numbers Together
Now that we can create Complex objects we can define other
behaviors (or functionality) for objects from the class. For example, suppose
we wanted to add two complex numbers together like this:
public static void main(String[] args) {
Complex c1 = new Complex(2.0, 1.0);
Complex c2 = new Complex(3.0, 8.0);
Complex sum = c1.plus(c2);
System.out.println(sum);
}
Here we intend for sum to contain the result of
adding c1 and c2 together. We can
define the plus() method in the Complex
class. The method accepts a Complex object as a parameter.
public class Complex {
// ...
public Complex plus(Complex addend) {
Complex sum = new Complex(real + addend.real, imag + addend.imag);
return sum;
}
}
In the previous paragraph, I said that the plus()
method accepts a Complex object as a parameter. That's really
a lie (an oversimplification). What it really accepts is a reference
to a Complex object. Let's take a moment to visualize what
is really going on in memory:
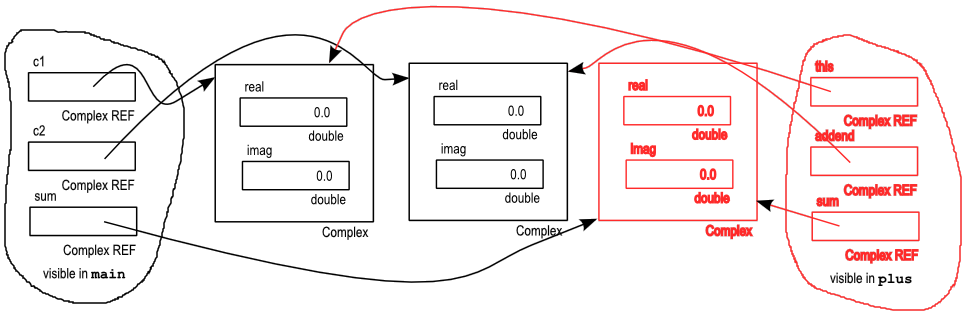
The three references c1, c2, and sum
are accessible in main() and the first two complex numbers were
instantiated from main() (all shown in black). The three
references this, addend, and sum
are accessible in the plus() method and the complex number
storing the result of adding the other two numbers together was instantiated
from the plus() method (all shown in red).
Java keyword this
In the above diagram the reference this magically
appeared. The this keyword is available whenever you
are in an object method and always points to the object that was used to
call the method. In the example above, that was c1. Making
use of the this keyword is often optional. For example,
we could rewrite the plus() method as follows and it will
function exactly the same way as before:
public Complex plus(Complex addend) {
return new Complex(this.real + addend.real, this.imag + addend.imag);
}
If this is not present, the compiler first looks for
a match to a local variable, and if none is present, it will then look for a
match to an object attribute. We could mess up the original plus()
method by creating a local variable called real.
public Complex plus(Complex addend) {
double real = 0.0;
return new Complex(real + addend.real, imag + addend.imag);
}
This is a problem because the real variable used when
creating the Complex object will be the local variable
(containing 0.0) instead of the value stored in the
attribute of the object. By using this we can
clarify that we mean the attribute of the object instead of the local
variable. As a result, this implementation (although having a useless
declaration of a local variable) will produce the desired result:
public Complex plus(Complex addend) {
double real = 0.0;
return new Complex(this.real + addend.real, this.imag + addend.imag);
}
Knowing this, we can improve the readability of our constructor by
using more descriptive labels for the parameters accepted by the constructor
(real instead of r and imag instead
of i):
public Complex(double real, double imag) {
this.real = real;
this.imag = imag;
}
Multiple Constructors
There may be times when we'd like to take a real number and convert it
into a Complex object. We could do that as follows:
double number = -2.0; Complex c1 = new Complex(number, 0.0);
It might be nice to make it a little easier for users of our
Complex class to do this. Instead of the above, we
could simplify it slightly by allowing them to say:
double number = -2.0; Complex c1 = new Complex(number);
In order to do this, we would need to create another constructor. This constructor accepts only one argument and sets the imaginary component to zero:
public Complex(double real) {
this.real = real;
this.imag = 0.0;
}
Calling Another Constructor
In an effort to minimize the amount of repeated code, we can have one constructor call another constructor. This allows us to do all of the initialization work in one place instead of having to repeat it in multiple places. Rewriting the above constructor as follows accomplishes this.
public Complex(double real) {
this(real, 0.0);
}
The above implementation instructs the compiler to generate code that will call the two-argument constructor passing the real value that was passed to this constructor and 0.0 for the imaginary component. In this particular example, the reduction in the amount of duplicate code is minimal, but this can have a more significant impact when implementing constructors for more complicated classes. It's a good idea to get in the habit of making calls to alternate constructors when possible.
One thing to keep in mind though, is that a call to another constructor must be the first thing you do in the constructor.
Constructor Accepting a String
Way back at the top of this page, I created a program asked the user
to enter two complex numbers and then displayed the result of multiplying
those numbers together. The code passed the user input into a
constructor for the Complex class that accepted a
String. That constructor is responsible for extracting the
real and imaginary components of the complex number from the string and
then initializing the real/imag attributes to the appropriate values.
public Complex(String num) {
Scanner parser = new Scanner(num.substring(0, num.length()-1));
real = parser.nextDouble();
parser.next();
imag = parser.nextDouble();
}
This assumes that the string will have the appropriate form:
"R + Ii" where R and I are
doubles (positive or negative). Later we'll
look at a more robust implementation.
In this case, we can't call the two argument constructor to initialize the object's attributes because we need to parse the string to figure out what the values should be. Since the call to another constructor must be the first operation, calling it is not an option for us here.
Almost There
Let's take a look back at the original program we were trying to write:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c1 = new Complex(in.nextLine());
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c2 = new Complex(in.nextLine());
System.out.println(c1 + " * " + c2 + " = " + c1.times(c2));
}
We can do everything here except the times() call
in the last print statement. The times() method is
very similar to the plus() method; it just does a
different calculation:
public Complex times(Complex multiplicand) {
return new Complex(this.real * multiplicand.real - imag * multiplicand.imag,
imag * multiplicand.real + real * multiplicand.imag);
}
I'm going to leave the implementation of minus() as a exercise
for now, but I'm confident you can write it, right?
Going Nuts
Suppose one of you classmates is a complex number guru, and she explains to you that complex number gurus insist that the-one-and-only-true-way to talk about complex numbers is using polar coordinates.1) As a result, you need to make it possible for complex numbers to be displayed using a polar coordinate system. We'd like to run the same program, but have the interaction with the user look like this:
Enter a complex number in the form: 3.0 + 4.3i 2.0 | 45.0 Enter a complex number in the form: 3.0 + 4.3i 8 | 90.0 (2.0 | 45.0) * (8.0 | 90.0) = (16.0 | -45.00000000000001)
Okay, maybe we should switch the prompts to suggest the appropriate form for entering the complex numbers, but I'm going to ignore that for now.
In order for us to be able to accept the polar form input, we
need to modify the constructor that accepts a String
so that it recognizes polar coordinates:
public Complex(String num) {
if(num.contains("|")) {
// In polar form, e.g., "1 | 45"
Scanner parser = new Scanner(num);
double magnitude = parser.nextDouble();
parser.next();
double angle = Math.toRadians(parser.nextDouble());
real = magnitude * Math.cos(angle);
imag = magnitude * Math.sin(angle);
} else {
// In cartesian form, e.g., "2.0 + 17.2i"
Scanner parser = new Scanner(num.substring(0, num.length()-1));
real = parser.nextDouble();
parser.next();
imag = parser.nextDouble();
}
}
In addition, we need to modify the way toString() works:
public String toString(){
return "(" + getMagnitude() + " | " + getAngle() + ")";
}
public double getMagnitude() {
return Math.sqrt(Math.pow(real, 2) + imag*imag);
}
public double getAngle() {
return Math.toDegrees(Math.atan(imag/real));
}
You'll notice a couple of additional methods here. I've decided to
make them public because users of the Complex class may
be interested in getting the magnitude or angle of the object.
Class Attributes/Methods
The change we made to the toString() method forces
the string representation of the object to be in polar coordinates,
and we no longer have the ability to get a string representation
in cartesian coordinates. It would be nice if we could switch between
both ways of representing these objects. (Just in case the self-proclaimed
complex number guru turns out to be a crack-pot.)
We'll do this by introducing an additional attribute for the
Complex class and two methods to control its value:
public class Complex {
// ...
private static boolean isPolar = false;
public static void setPolar() {
isPolar = true;
}
public static void setCartesian() {
isPolar = false;
}
// ...
}
You'll notice that all of these are declared with the
static modifier. Such a declaration
indicates that the attribute/method is not associated
with a specific object but is associated with the class
instead. As a result, you do not need a Complex
object in order to call a static
method and all Complex objects share the
same attribute value.
We can now modify the toString() implementation
so that it generates a string in polar form if
isPolar is true; otherwise, it
will generate a string in cartesian form:
public String toString(){
String answer = "(" + real + " + " + imag + "i)";
if(isPolar) {
answer = "(" + getMagnitude() + " | " + getAngle() + ")";
}
return answer;
}
Now we'll add a line to our program that calls
setPolar() in order to set our preference
for the toString() method to produce
strings representing the objects in polar coordinates.
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
Complex.setPolar();
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c1 = new Complex(in.nextLine());
System.out.println("Enter a complex number in the form: 3.0 + 4.3i");
Complex c2 = new Complex(in.nextLine());
System.out.println(c1 + " * " + c2 + " = " + c1.times(c2));
}
Because isPolar() is associated with the class, we
call it using the name of the class instead of the name of an
object from the class. This sets the class attribute
isPolar to true and, since all
objects share that same value, all calls to the
toString() method will generate strings in polar form
(until Complex.setCartesian() is called).
Running our program now will produce the following interaction:
Enter a complex number in the form: 3.0 + 4.3i 2.0 | 45.0 Enter a complex number in the form: 3.0 + 4.3i 8.0 | 90 (2.0 | 45.0) * (8.0 | 90.0) = (16.0 | -45.00000000000001)
Using Polar Coordinates for dividedBy()
Even though your annoying classmate forced us to do all
this work related to polar coordinates, there is a bright side:
it will make it easier for us to implement the
dividedBy() method since division of complex numbers
is easier when the numbers are represented in polar form.
public Complex dividedBy(Complex divisor) {
double magnitude = getMagnitude() / divisor.getMagnitude();
double angle = Math.toRadians(getAngle() - divisor.getAngle());
return new Complex(magnitude * Math.cos(angle), magnitude * Math.sin(angle));
}
Alternatively, we could make use of our constructor that accepts a
string to create the new Complex object:
public Complex dividedBy(Complex divisor) {
double magnitude = getMagnitude() / divisor.getMagnitude();
double angle = getAngle() - divisor.getAngle();
return new Complex(magnitude + " | " + angle);
}
A Brief Retrospective
At the top of this page, we started with a non-OO approach. This program was complicated and not very robust. For example, if the user entered -2.3i for the complex number, the program wouldn't work. We were able to simplify the code significantly by re-writing it using an OO approach and a class to represent complex numbers.
Our first iteration of the Complex class would also get
confused if the user entered -2.3i for one of the complex numbers;
however, by improving the implementation of the Complex class,
our program can now handle such an input.
This is a big deal! The program got better without requiring
any changes to my code. I just needed to convince the developer of my
Complex class to make improvements.
Putting it All Together
The complete Complex class is shown below. I've made a few
additional improvements:
- Added Javadoc comments.
- Improved the format of cartesian-coordinate output from
toString(). - Updated the string based constructor to be more robust.
- Other little things (think of it as a treasure hunt).
/*
* SE1011-061
* Fall 2015
* Tutorial on User-Built Classes
* Name: Dr. Chris Taylor
* Created: 10/30/2015
*/
package us.msoe.se1011;
/**
* Represents complex numbers. Objects from the class are immutable,
* i.e., their value cannot change once they are created.
* @author taylor
* @version 2015.10.30_2
*/
public class Complex {
/**
* Real component of the complex number
*/
private final double real;
/**
* Imaginary component of the complex number
*/
private final double imag;
/**
* Determines whether the string representation of the complex number
* will be in cartesian or polar coordinates
*/
private static boolean isPolar = false;
/**
* Default constructor of a complex number with real and
* imaginary components of zero
*/
public Complex() {
this(0.0);
}
/**
* Constructor of a complex number with an imaginary component of zero
* @param real The value of the real component
*/
public Complex(double real) {
this(real, 0.0);
}
/**
* Constructor for a fully specified complex number
* @param real The value of the real component
* @param imag The value of the imaginary component
*/
public Complex(double real, double imag) {
this.real = real;
this.imag = imag;
}
/**
* Constructor that accepts a string representation of a
* complex number
* @param num String representation of a complex number
*/
public Complex(String num) {
double real = 0.0;
double imag = 0.0;
num = num.replace("(", "").replace(")", "");
if(num.contains("|")) {
// In polar form, e.g., "1 | 45"
Scanner parser = new Scanner(num);
double magnitude = parser.nextDouble();
parser.next();
double angle = Math.toRadians(parser.nextDouble());
real = magnitude * Math.cos(angle);
imag = magnitude * Math.sin(angle);
} else if(num.contains(" + ") || num.contains(" - ")) {
// Both real and imaginary components present, e.g., "2.0 - 2.0i"
Scanner parser = new Scanner(num.substring(0, num.length()-1));
real = parser.nextDouble();
parser.next();
imag = parser.nextDouble();
if(num.contains(" - ")) {
imag = -imag;
}
} else if(num.contains("i")) {
// imaginary component only, e.g., "3.8i"
Scanner parser = new Scanner(num.substring(0, num.length()-1));
imag = parser.nextDouble();
} else {
// real component only, e.g., "-5.6"
Scanner parser = new Scanner(num);
real = parser.nextDouble();
}
this.real = real;
this.imag = imag;
}
/**
* The String representation of the complex number
* This may be in cartesian or polar form depending on
* the value of the class variable isPolar.
* @see Object#toString()
* @return String representation of the object
*/
public String toString(){
String answer;
if(!isPolar) {
if(this.imag==0.0) {
answer = Double.toString(real);
} else if(this.real==0.0) {
answer = imag + "i";
} else if(this.imag<0.0) {
answer = "(" + real + " - " + (-imag) + "i)";
} else {
answer = "(" + real + " + " + imag + "i)";
}
} else {
answer = "(" + getMagnitude() + " | " + getAngle() + ")";
}
return answer;
}
/**
* Calculates the sum of the object and a real value
* @param addend The value to be added to the real component of the complex number
* @return A new complex number containing the sum of the object and the specified
* real component
*/
public Complex plus(double addend) {
return new Complex(this.real + addend, this.imag);
}
/**
* Calculates the sum of two complex numbers
* @param addend Number to be added
* @return the result of the sum of two complex numbers
*/
public Complex plus(Complex addend) {
return new Complex(this.real + addend.real, this.imag + addend.imag);
}
/**
* Calculates the difference of two complex numbers
* @param subtrahend Number to be subtracted
* @return the result of taking away the specified value from the object
*/
public Complex minus(Complex subtrahend) {
return new Complex(real - subtrahend.real, imag - subtrahend.imag);
}
/**
* Compares two complex numbers to see if they are equal
* @param that The complex number to compare
* @return true if the objects share the same value, otherwise false
*/
public boolean equals(Complex that) {
return this.real==that.real && this.imag==that.imag;
}
/**
* Returns the magnitude of the complex number
* @return the magnitude of the complex number
*/
public double getMagnitude() {
return Math.sqrt(Math.pow(real, 2) + imag*imag);
}
/**
* Returns the angle of the complex number in degrees
* @return the angle of the complex number in degrees
*/
public double getAngle() {
return Math.toDegrees(Math.atan(imag/real));
}
/**
* Sets class preference so that complex numbers are represented in
* polar coordinates
*/
public static void setPolar() {
isPolar = true;
}
/**
* Sets class preference so that complex numbers are represented in
* cartesian coordinates
*/
public static void setCartesian() {
isPolar = false;
}
/**
* Calculates the product of two complex numbers
* @param multiplicand Number to be multiplied
* @return the result of the product of two complex numbers
*/
public Complex times(Complex multiplicand) {
return new Complex(this.real * multiplicand.real - imag * multiplicand.imag,
imag * multiplicand.real + real * multiplicand.imag);
}
/**
* Calculates the result of dividing the passed complex number
* into the calling number
* @param divisor Number to be used as the divisor
* @return the result of the division
*/
public Complex dividedBy(Complex divisor) {
double magnitude = getMagnitude() / divisor.getMagnitude();
double angle = Math.toRadians(getAngle() - divisor.getAngle());
return new Complex(magnitude * Math.cos(angle), magnitude * Math.sin(angle));
}
}
Last modified: Monday, 29-Jul-2024 06:55:07 EDT