CS3851 -- Homework

[an error occurred while processing this directive]

Overview

You are encouraged to work on the homework in groups; however, each student is required to submit solutions to each homework assignment. During the lecture period immediately after the homework assignment has been announced, the class may select one problem to be removed from the assignment (provided at least half of the class can summarize the problem statement for the problem being removed).

Each problem will be graded on the following scale:

• -3 points: substantially incorrect
• 0 points: minor mistakes, unorganized, or unclear
• 3 points: Clearly presented and correct

When calculating your final grade, I will add your average homework problem score to your lab/exam grade. For example, suppose your grade for all exams and lab assignments is 86.3%. If you do not turn in any homework, your final grade will be 83.3% (BC). If you submit correct and clearly presented solutions to all of the problems, your final grade will be 89.3% (AB).

Homework is due at the beginning of the class period indicated. (The one hour grace period does not apply.)

Specific Assignments

HW 1: Week 2 Lecture 3

1. Give an example of where sort is used out in the wild.
2. Suppose you are comparing implementations of two sorting algorithms running on the same machine. For what value of \(n\) (the input size), does an algorithm that runs in \(8n^2 + 3n + 8\) run faster than an algorithm that runs in \(64n\lg n + 37n + 6\)? Hint: consider graphing each equation.
3. Illustrate the operation of Insertion-Sort on the following array: A = {37, 41, 87, 27, 41, 81}. Use Figure 2.2 in the textbook as a model.
4. Express \(n^3/1234 - 567n^2 - 89n + 87\) in terms of \(\Theta\)-notation.
5. Illustrate the operation of Merge-Sort on the following array: A = {37, 41, 87, 27, 41, 81}. Use Figure 2.4 in the textbook as a model.
6. (Done in class) Problem 2-1
7. Suppose \(a(n)\) and \(b(n)\) are nonnegative functions. Prove that \(max(a(n),b(n)) = \Theta(a(n)+b(n))\) using the basic definition of \(\Theta\)-notation.

HW 2: Week 3 Lecture 2

1. Simplify the following expression as much as possible: \(\sum_{k=1}^{n}(4k+2)\)
2. Show that the following expression is never larger than a constant value (regardless of how large \(n\) becomes): \(8 + \sum_{k=1}^{n}(\frac{1}{k^2})\)
3. Show that the solution of \(T(n) = T(\lceil n/2 \rceil ) + 1\) is \(O(\lg n)\) a) using iteration and b) using induction
4. Use the master method to give tight asymptotic bounds for the following recurrences:
   1. \(T(n) = 9T(n/3) + n\)
   2. \(T(n) = 9T(n/3) + n^2\)
   3. \(T(n) = 9T(n/3) + n^3\)
5. Consider the recurrence: \(T(n) = 9T(n/3) + n^2 \lg n\) Can the master method be applied to solving this recurrence? Why or why not?
6. Typically we assume that parameter passing during method calls takes constant time, even if an N-element array is being passed. This assumption is valid for Java since a reference to the array is passed, not a copy of the array. This problem examines the implications of three parameter-passing strategies:
   1. An array passed by reference. Time = \(\Theta(1)\).
   2. An array passed by copying. Time = \(\Theta(N)\), where N is the size of the original array.
   3. An array passed by copying only the subrange that might be accessed by the called procedure. Time = \(\Theta(q-p+1)\), if the subarray A[p .. q] is passed.
   Consider the recursive binary search algorithm for finding a number in a sorted array. Give recurrences for the worst-case running times of binary search when arrays are passed using each of the three methods above, and give good upper bounds on the solutions of the recurrences. Let N be the size of the original problem and n be the size of a subproblem.
7. Consider the recursive Merge-Sort algorithm. Give recurrences for the worst-case running times of Merge-Sort when arrays are passed using each of the three methods in the previous problem, and give good upper bounds on the solutions of the recurrences. Let N be the size of the original problem and n be the size of a subproblem.

HW 3: Week 4 Lecture 2

1. What are the minimum and maximum numbers of elements for a heap of height \(h\)?
2. Is an array that is sorted in ascending order a min-heap? Why or why not?
3. Illustrate the operation of Max-Heapify(A, 3) on the following array: A = {35, 48, 72, 12, 47, 88, 5, 12, 10, 45}. Use Figure 6.2 in the textbook as a model.
4. Suppose that A[\(i\)] is larger than its childern. How does the array differ after calling Max-Heapify(A, i)? Why?
5. How does the array differ after calling Max-Heapify(A, i) when \(i\) is greater than half the size of the heap? Why?
6. Why do we want \(i\) in line 2 of Build-Max-Heap to decrease from \(\lfloor length[A]/2\rfloor\) to 1 instead of increasing from 1 to half the length of A?
7. What is the running time of heapsort on an array of length \(n\) that is already sorted in ascending order? What is the running time of heapsort on an array of length \(n\) that is already sorted in descending order?
8. Illustrate the operation of Partition(A, 1, \(length(A)\)) on the following array: A = {35, 48, 72, 12, 47, 88, 5, 12, 10, 45}. Use Figure 7.1 in the textbook as a model.
9. What value does Partition(A, p, r) when all of the values in A are identical?
10. What is the running time of Quicksort(A, 1, \(length(A)\)) when all of the values in A are identical?
11. (Done in class) Consider the number of calls to the random number generator when running Randomized-Quicksort(A, 1, \(length(A)\)). Using \(\Theta\)-notation, give the best-case number of calls. Using \(\Theta\)-notation, give the worst-case number of calls.

HW 4: Week 5 Lecture 3

1. Show that the second smallest of \(n\) elements can be found with no more than \(n + \lceil \lg n \rceil - 2\) comparisons. (Hint: Also find the smallest element.)
2. Illustrate the worst-case (unluckiest) operation of Randomized-Select(A, 1, \(length(A)\), 1) on the following array: A = {33, 45, 72, 10, 44, 60}.
3. Problem 9-1
4. Suppose that the frequency of the symbols is based on the Fibonacci sequence, e.g., a:1 b:1 c:2 d:3 e:5 f:8 g:13 h:21. For the symbols listed, find the optimal Huffman code for each symbol. Attempt to generalize the optimal Huffman codes for \(n\) symbols whose frequencies follow the Fibonacci sequence.
5. Provide a convincing argument that if we order the characters in the alphabet so that their frequencies are monotonically decreasing, then there exists an optimal code whose codeword lengths are monotonically increasing.

HW 5: Week 7 Lecture 1

1. Suppose a directed graph, \(G = (V, E)\), is described using an adjacency-list. How long does it take to compute the out-degree of every vertex? How long does it take to compute the in-degree of every vertex? Justify your answers.
2. Consider a complete binary tree with vertices number from one to seven. Show its adjacency-list and adjacency-matrix representations.
3. Using vertex A as the source, show the \(d\) and \(\pi\) values that result from running breadth-first search on the following directed graph
   
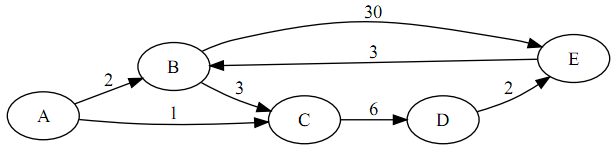
4. Provide a convincing argument that the breadth-first search algorithm could get by with only two colors for the vertices. What lines of the BFS(G, s) algorithm presented in the book could be eliminated without rendering it ineffective?
5. Selecting the node earliest in the alphabet whenever there is a choice, demonstrate running depth-first search on the following directed graph. Be sure to show the discovery and finishing times for each vertex and the classification of each edge.
   
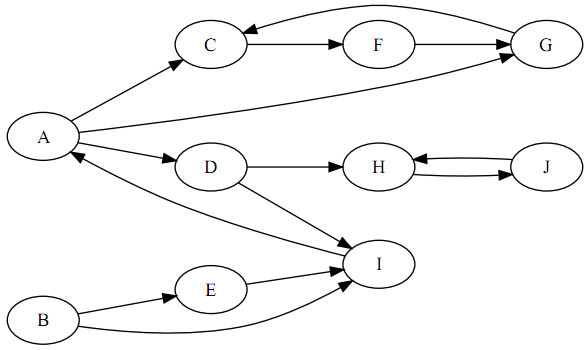
6. Illustrate the operation of Kruskal's algorithm on the following graph. Identify each edge and its corresponding weight as you work through the algorithm.
   
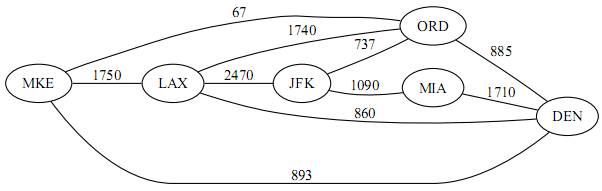
7. Illustrate the operation of Prim's algorithm on the graph in the previous problem.
8. Give an example of a direct graph with negative edges and no more than five vertices for which Dijkstra's algorithm produces incorrect answers.

HW 6: Week 9 Lecture 3

1. Find an optimal parenthesization of a matrix-chain product whose sequence of dimensions is \(\langle 5, 8, 8, 12, 8, 50, 5 \rangle\).
2. Suppose that Dr. Hornick has a standard deck of 52 playing cards (26 are red and 26 are black). Dr. Hornick turns over the cards one at a time. Dr. Uphoff starts with $100. Before each card is flipped, Dr. Uphoff can bet any whole dollar amount ($0 to his current total) on the color of the next card. Assuming even odds (that's right, even odds) regardless of the current composition of the deck. What is the most Dr. Uphoff can guarantee to end up with?
   For example, Dr. Uphoff can guarantee $200 by betting $0 on the first 51 cards and $100 on the last card (since he can count how many of each color have already been shown). Create a dynamic programming solution and actually code it up. You may work with your lab partner(s) on this problem. Provide one solution for all who participated in its creation.
3. Problem 15-4
4. Consider the 0-1 knapsack problem. Give a dynamic-programming solution that runs in \(O(n W)\) time, where \(n\) is the number of items and \(W\) is the maximum weight of items that can be put in the knapsack.
5. Exercise 16.2-4
6. Problem 16-1a&c
7. Exercise 34.1-1
8. Is your dynamic-programming solution to the 0-1 knapsack problem above a polynomial-time algorithm? Why or why not?